[내일배움캠프] 31일 차 - SQL 코드카타, 데이터 전처리&시각화 5, 통계 특강 1강

 

 

 

 SQL 코드카타

 

 

문제 70

그룹별 조건에 맞는 식당 목록 출력하기

 

☑ link

 

 

최종 답안

SELECT C.MEMBER_NAME, -- 6. 최종적으로 리뷰 수 최대인 사람의 3가지 정보만 출력
       C.REVIEW_TEXT,
       C.REVIEW_DATE
FROM      
(
    SELECT A.MEMBER_NAME, -- 4. A, B JOIN 결과에 대해 윈도우 함수로 순위 구하기
           A.REVIEW_TEXT,
           DATE_FORMAT(A.REVIEW_DATE, '%Y-%m-%d') AS REVIEW_DATE,
           RANK() OVER(ORDER BY B.COUNT_REVIEW DESC) AS RANKING
    FROM 
    (
        SELECT M.MEMBER_NAME, -- 1. 최종적으로 출력해야 할 컬럼들
               R.REVIEW_TEXT,
               R.REVIEW_DATE,
               M.MEMBER_ID
        FROM MEMBER_PROFILE M
        JOIN REST_REVIEW R
        ON M.MEMBER_ID = R.MEMBER_ID
    ) A
    JOIN -- 3. 집계함수 규칙 때문에 A, B를 따로 구한 뒤 JOIN
    (
        SELECT MEMBER_ID, -- 2. 회원별 리뷰 수 집계
               COUNT(REVIEW_ID) AS COUNT_REVIEW
        FROM REST_REVIEW
        GROUP BY MEMBER_ID
    ) B
    ON A.MEMBER_ID = B.MEMBER_ID
) C
WHERE C.RANKING = 1 
-- 5. C에서 구한 순위 중 1위만 남겨 리뷰 수 최대인 사람만 남김 (중복가능)
ORDER BY C.REVIEW_DATE, C.REVIEW_TEXT

 

쿼리의 흐름 정리

 

1. 서브쿼리 A

최종적으로 출력해야 할 컬럼들

         ↓

2. 서브쿼리 B

회원별 리뷰 수 집계

         ↓

3. 집계함수 규칙 때문에 A, B를 따로 구한 뒤 JOIN

         ↓

4. 서브쿼리 C

A, B의 JOIN 결과에 대해 윈도우 함수로 순위 구하기

         ↓

5. 서브쿼리 C
윈도우 함수 RANK로 구한 순위 중 1위만 남겨 리뷰 수 최대인 사람만 남김 (중복가능)

         ↓

6. 본쿼리

최종적으로 리뷰 수 최대인 사람의 3가지 정보만 출력

 

 

 

 데이터 전처리 & 시각화 Pandas - 5

 

 

 

데이터 전처리 & 시각화 강의 3주차 : Pandas 위주로 정리 - 4

 

7. 데이터 전처리 - 데이터 집계

 

1) groupby()

• 데이터프레임 그룹화하고,
  그룹 단위로 데이터를 분할(split), 적용(apply), 결합(comebine)
• 데이터프레임을 특정 기준에 따라 그룹으로 나누어 집계, 변환, 필터링
  1. 그룹 생성
     기준 열(혹은 열 여러 개)을 지정하여 데이터프레임을 그룹으로 나눔
  2. 그룹에 대한 연산 수행
     그룹 단위로 원하는 연산 수행: 평균, 합, 개수 등
  3. 결과 결합
     각 그룹의 연산 결과를 하나의 데이터프레임으로 결합
• 복수의 열 기준으로 그룹화하는 경우
  • groupby() 함수에 복수의 열 리스트로 전달해 
    원하는 그룹화 기준 지정
  • agg() 함수 사용해 
    여러 열에 대해 다양한 집계 함수 적용

 

• groupby 함수 예시

import pandas as pd

# 샘플 데이터프레임 생성
data = {
    'Category': ['A', 'B', 'A', 'B', 'A', 'B'],
    'Value': [1, 2, 3, 4, 5, 6]
}
df = pd.DataFrame(data)

# 'Category' 열을 기준으로 그룹화하여 'Value'의 연산 수행
grouped = df.groupby('Category').mean()

grouped_sum = df.groupby('Category').sum()
grouped_count = df.groupby('Category').count()
grouped_max = df.groupby('Category').max()
grouped_min = df.groupby('Category').min()

# 수치형 데이터의 경우에 연산이 가능

• 복수의 열 기준으로 groupby 함수 사용

import pandas as pd

data = {
    'Category': ['A', 'A', 'B', 'B', 'A', 'B'],
    'SubCategory': ['X', 'Y', 'X', 'Y', 'X', 'Y'],
    'Value': [1, 2, 3, 4, 5, 6]
}
df = pd.DataFrame(data)

# 'Category'와 'SubCategory' 열을 기준으로 그룹화해 'Value'의 합 계산
grouped_multiple = df.groupby(['Category', 'SubCategory']).sum()

print(grouped_multiple)

• 다양한 집계 함수 적용

import pandas as pd

data = {
    'Category': ['A', 'A', 'B', 'B', 'A', 'B'],
    'SubCategory': ['X', 'Y', 'X', 'Y', 'X', 'Y'],
    'Value1': [1, 2, 3, 4, 5, 6],
    'Value2': [10, 20, 30, 40, 50, 60]
}
df = pd.DataFrame(data)

# 'Category'와 'SubCategory' 열을 기준으로 그룹화
# 각 그룹별 'Value1'의 평균과 합, 'Value2'의 합 계산
grouped_multiple = df.groupby(['Category', 'SubCategory']).agg({'Value1': ['mean', 'sum'], 'Value2': 'sum'})

print(grouped_multiple)

'''
복수의 열을 기준으로 그룹화하여 데이터프레임을 조작하는 경우, 
groupby() 함수에 복수의 열을 리스트로 전달하여 원하는 그룹화 기준을 지정, 
agg() 함수를 사용하여 여러 열에 대해 다양한 집계 함수를 적용
'''

 

 

2) Pivot Table

 

• pivot_table()
• 주어진 데이터 사용자가 원하는 형태로 재배치해 요약된 정보 보기 쉽게 제공

 

• 피벗 테이블 생성

import pandas as pd

data = {
    'Date': ['2023-01-01', '2023-01-01', '2023-01-02', '2023-01-02', '2023-01-01'],
    'Category': ['A', 'B', 'A', 'B', 'A'],
    'Value': [10, 20, 30, 40, 50]
}
df = pd.DateFrame(data)

# 피벗 테이블 생성: 날짜를 행 인덱스로, 카테고리를 열 인덱스로,
# 값은 'Value'의 합으로 집계
pivot = df.pivot_table(index='Date', columns='Category', values='Value', aggfunc='sum')

print(pivot)

• 여러 열 기준으로 피벗 테이블 생성

import pandas as pd

data = {
    'Date': ['2023-01-01', '2023-01-01', '2023-01-02', '2023-01-02', '2023-01-01'],
    'Category': ['A', 'B', 'A', 'B', 'A'],
    'SubCategory': ['X', 'Y', 'X', 'Y', 'X'],
    'Value': [10, 20, 30, 40, 50]
}
df = pd.DataFrame(data)

# 피벗 테이블 생성: 'Date'를 행 인덱스로,
# 'Category'와 'SubCategory'를 열 인덱스로,
# 값은 'Value'의 합으로 집계
pivot = df.pivot_table(index='Date', columns=['Category', 'SubCategory'], values='Value', aggfunc='sum')

print(pivot)

• 집계 함수 다르게 적용해 피벗 테이블 생성

import pandas as pd

data = {
    'Date': ['2023-01-01', '2023-01-01', '2023-01-02', '2023-01-02', '2023-01-01'],
    'Category': ['A', 'B', 'A', 'B', 'A'],
    'Value1': [10, 20, 30, 40, 50],
    'Value2': [100, 200, 300, 400, 500]
}
df = pd.DataFrame(data)

# 피벗 테이블 생성: 'Date'를 행 인덱스로,
# 'Category'를 열 인덱스로,
# 값은 'Value1'의 평균과 'Value2'의 합으로 집계

pivot = df.pivot_table(index='Date', columns='Category', values=['Value1', 'Value2'], aggfunc={'Value1': 'mean', 'Value2': 'sum'})

print(pivot)

 

 

8. 데이터 전처리 - 데이터 정렬

 

1) sort_values()

• 컬럼 기준으로 정렬

import pandas as pd

data = {
    'Name': ['Alice', 'Bob', 'Charlie', 'David', 'Eva'],
    'Age': [25, 22, 30, 18, 27],
    'Score': [85, 90, 75, 80, 95]
}
df = pd.DataFrame(data)

# 정렬
sorted_by_score = df.sort_values('Score') # 오름차순
sorted_by_score = df.sort_values('Score', ascending=False) # 내림차순

print(sorted_by_score)

 

2) sort_index()

• 인덱스 기준으로 정렬

import pandas as pd

data = {
    'Name': ['Alice', 'Bob', 'Charlie', 'David', 'Eva'],
    'Age': [25, 22, 30, 18, 27],
    'Score': [85, 90, 75, 80, 95]
}
df = pd.DataFrame(data)

# 정렬
sorted_by_index = df.sort_index()  # 인덱스 기준 오름차순 정렬
sorted_by_index = df.sort_index(ascending=False)  # 인덱스 기준 내림차순 정렬

print(sorted_by_index)

 

자료 출처

스파르타 코딩클럽 데이터 전처리 & 시각화 강의

 

 

 

 

 통계 특강 1강

 

 

 

통계 특강 1강 - 곽승예 튜터님

 

0. 통계 왜 배워야 할까?

 

통계란?

• 데이터는 사실,
  통계는 그 사실을 해석하는 도구
  • 사실 : 하루 방문자 수가 1,000명에서 600명으로 줄었다.
  • 해석 : 최근 메인 페이지 UI 개편 후 진입률이 감소했을 수 있다.
    • 그 수치에 맥락을 붙여 ‘이유’를 설명하는 게 해석
      = 해석은 주관이 들어감
    • 통계는 이 해석을 위한 논리적 도구

 

배우는 이유

• 데이터 분석가는 사실을 전달하는 사람이 아닌, 그 사실을 바탕으로 의사결정의 근거를 만들고, 설득하는 사람
  • ❌ “여성 고객이 더 제품을 많이 사는 것 같아요”
  • ⭕️ “100명 중 85%의 사용자가 여성이고, 이들의 평균 구매 금액은 남성 고객의 두 배 이상입니다. 따라서 여성 고객을 타겟으로 프로모션을 진행해야 합니다.”

• 통계를 배우는 이유는?
  • 데이터를 이해하기 위해 → 이상값, 분포, 편향 등 확인, 판단
  • 다른 사람을 설득하기 위해 → 명확한 수치와 통계적 근거로 이야기하기
  • 모델링과 머신러닝의 기반 → 선형 회귀, 분류, 확률 등 통계적 개념에 기반한 모델들 이해하기
  • 신뢰할 수 있는 추론과 검증 위해 → 우연인지, 의미 있는 차이인지 구분하기

 

 

1. 통계 기초

통계학의 목적: 모집단의 성질을 추정하고 설명하는 것

 

1) 모집단과 표본

• 모집단: 통계학에서 알고자 하는 대상 전체
  • 모집단의 데이터를 얻을 수 없기에, 현재 가진 데이터로 모집단을 추정함
• 모집단 추정하는 방법
  • 전수 조사: 모집단에 포함된 모든 요소 조사
  • 표본 조사: 모집단의 일부 분석 → 모집단 전체 성질 추정
    • 표본: 모집단의 일부
    • 표본 추출: 모집단에서 표본 뽑는 것
    • 표본 크기: 표본에 포함된 요소의 개수 (샘플 수)

2) 기술 통계와 추론 통계

 

2-1) 기술 통계 (Descriptive Statistics)

 

기술 통계

• 현재의 데이터를 요약하고 설명(기술)하는 통계
• 관찰된 데이터에 집중
• 중심 경향치: 평균, 중앙값, 최빈값

 

중심극한정리 (Central Limit Theorem)

• 모집단의 분포 형태와 상관없이 충분히 큰 크기의 표본을 여러 번 추출해 표본 평균들을 구하면
  표본평균들의 분포는 정규분포에 가까워진다.
• 추론 통계: 표본평균들의 분포(표본분포)로 모집단의 평균을 추정할 수 있다
  
  • 모집단에서 표본 1 뽑음
  • 표본 1의 평균 구함
  • 또 다시 모집단에서 표본 2 뽑음
  • 표본 2의 평균 구함
  • 반복
  • 표본 평균들로 이루어진 데이터 구함: 표본1의 평균, 표본 2의 평균, · · ·표본 n의 평균
• 표준오차: 표본 평균의 분포의 퍼짐(변동성)을 나타내는 값
• 표준오차가 작다: 표본평균들이 모여 있음
• 표준오차가 크다: 표본평균들이 흩어져 있음

 

데이터의 흩어진 정도: 분산, 표준편차

• 편차 (Deviation)
  각 데이터가 평균에서 얼마나 떨어져 있는지
• 분산 (Variance)
  편차 제곱의 평균
• 표준편차 (Standard Deviation)
  분산에 루트 씌운 값
• 분산 확인할 수 있는 시각화
  히스토그램, box plot, 밀도 곡선, 바이올린 플랏

 

표준편차와 표준오차의 차이

• 표준편차
  • 관측값들의 퍼짐
  • 데이터들이 평균으로부터 얼마나 떨어져 있는지
• 표준오차
  • 표본 통계량의 퍼짐
  • 주로 표본평균들이 모평균으로부터 얼마나 떨어져 있는지

 

분포

• 왜도
  데이터 분포 좌우 비대칭성 나타내는 척도
• 첨도
  뾰족함이나 완만함 정도 나타내는 척도

 

 

2-2) 추론 통계 (Inferential Statistics)

• 일부 데이터(표본)을 바탕으로 전체 모집단을 추정하거나
  어떤 주장이 맞는지 검정하는 통계
• 확률로 불확실성을 다루는 통계
• 기술 통계: 관측된 데이터 요약
  추론 통계: 관측되지 않은 모집단을 예측
• 표본이 얼마나 신뢰할 수 있는 정보인지 추정할 때, 확률을 사용
  • 표본 평균이 모집단의 평균과 얼마나 비슷할까?
  • 표본 평균과 모집단의 평균의 차이는 우연일까 유의미한 차이일까?

 

데이터 분석에서 기술 통계와 추론 통계가 사용되는 방법

1. 데이터 수집/정리
2. 기술 통계: 요약 및 탐색
3. 추론 통계: 예측, 검정, 일반화
4. 인사이트 도출 & 의사결정

통계학 관점에서 데이터 바라보기

• 확률분포 추정: 데이터가 어떤 확률분포 따르는지 파악
• 상관관계, 인과관계 분석: 두 변수 간 관계가 우연인지 통계적으로 유의미한지 파악
• 예측 모델링: 하나의 독립 변수로 다른 종속 변수 예측

→  표본을 통해 모집단의 특성, 변수 간 관계 등을 예측 및 검정

 

 

2. 확률 기초

 

1) 확률

 

확률

• 발생 여부 불확실한 사건의 발생 가능성 숫자로 표현
• 0 ≤ P(A) ≤ 1
• 모든 사건의 확률 전부 더하면 1

 

확률변수

• 사건의 결과에 따라 값이 확률적으로 정해지는 변수 
• 결과가 나오기 전에는 어떤 값이 나올지 모르지만,
  그 값들이 나올 확률은 알고 있는 경우
  • 이산형 확률변수
    하나씩 셀 수 있는 변수
    가능한 값이 유한함
    주사위, 나이 등
  • 연속형 확률변수
    무한하게 정밀하게 쪼개는 것 가능한 변수
    특정 구간 내에 연속적으로 존재
    키, 수면시간 등
• 실현값
  실제로 그 확률변수가 가진 구체적인 값
  공을 뽑았을 때 결과값이 초록색

 

2) 확률분포

 

확률분포

• 확률변수가 가질 수 있는 값과 그에 대한 발생 확률 간의 관계를 정리한 것
• x축: 확률변수
• y축: 그 값이 나올 가능성 (확률 또는 밀도)

 

이산형 확률분포

• 셀 수 있는 값
• 유한 개
• 막대 그래프

 

연속형 확률분포

• 연속적인 값
• 무한 개
• 부드러운 곡선
• 특징
  • 특정한 한 점의 값의 확률은 0이다
    소수점 이하 자리가 무한히 계속될 수 있으므로
  • 구간으로 확률 계산해야 한다 → 적분

 

확률분포는 왜 추론통계에서 중요할까?

• 현실의 모집단은 관찰 불가능하므로
  확률분포로 가정한다
• 이때 우리가 수집한 데이터(표본)는
  이 분포에서 나온 실현값이라고 생각한다
• 통계적 추론: 실현값을 바탕으로 어떤 분포에서 나왔는지 추정하는 과정
• 데이터를 통해, 그 데이터를 만들어낸 '보이지 않는 분포'를 알아내려는 것

 

 

3) 기댓값 (expected value)

• 확률변수를 오래 반복했을 때 평균적으로 기대되는 값

 

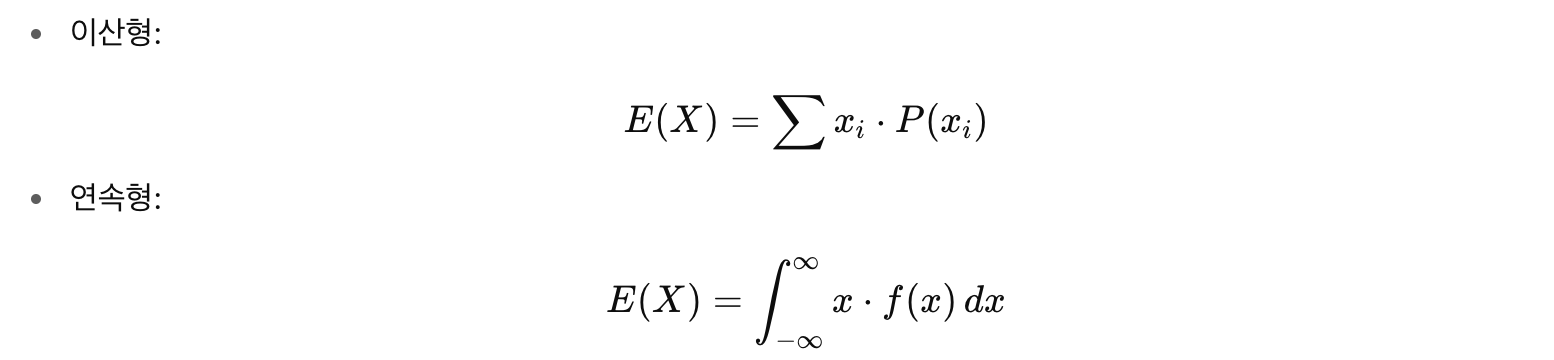
4) 조건부확률

 

동시확률분포

• 확률변수 2개를 동시에 생각할 때의 확률분포
• 독립: 2개의 확률변수에 대한 동시확률분포 P(X, Y) = P(X) * P(Y)
  • 한쪽이 어떤 값을 취하든, 다른 한 쪽의 발생 확률은 변하지 않음

 

조건부확률

• P(X | Y)
  Y라는 정보가 주어졌을 때, X가 일어날 조건부 확률
• Y에 대한 정보가 생기면, X에 대한 불확실성을 줄일 수 있다. 
  Y의 정보로 X의 확률 달라짐

 

독립과 의존

• 독립 (Independent)
  
  • X, Y가 서로 영향 주지 않음
  • P(X | Y) = P(X)
• 의존 (Dependent)
  • Y의 정보가 X의 확률을 바꿈
  • P(X | Y) ≠ P(X)

 

조건부확률 활용: 추론 상황과 조건부확률적 해석

• 가설 검정
  귀무가설이 참이라는 조건 하에 이 결과가 나올 확률은?
• 신뢰구간
  이 표본 평균이 주어졌을 때 모평균이 들어갈 수 있는 범위는?
• 모형 예측
  X를 알 때, Y가 나올 확률은?
• 베이즈 추론
  데이터를 관측한 뒤 어떤 가설이 맞을까?

 

베이즈 정리 (Bayes' Theorem)

• 베이즈 정리: 이미 알고 있는 정보(조건)을 바탕으로,
  어떤 사건이 일어났을 가능성(사후확률)을 계산
• 조건부확률을 거꾸로 바꿔서 구함

 

• 베이즈 정리의 유용함
  • 조건부확률
    • P(A | B)
    • A는 우리가 알고 싶은 원인, B는 관측한 결과
    • 특정 사건 (B)이 발생했다는 전제 하에 다른 사건 (A)이 발생할 확률
    • P(광고 | 구매)
      전제: 구매 내역 데이터가 있음
      구하고 싶은 것: 구매한 사람들 중 광고를 본 사람이 몇 명인지
  • 베이즈 정리
    • P(A | B)를 알고 있을 때, 이를 이용해 P(B | A) 구함
    • 결과를 통해 그 원인을 확률적으로 추론할 수 있다
    • P(구매 | 광고)
      광고를 본 사용자가 구매했을 확률
      원인: 광고를 봄
      결과: 구매함
      조건부확률 P(광고 | 구매)를 사용해 해당 확률 구할 수 있음

 

 

3. 추론 통계

 

추정과 가설검정

• 추정 (Estimation)
  • 모집단의 평균, 비율을 알 수 없기에 표본을 통해 추정함
  • 범위로 표현함 (=신뢰구간)
  • 평균 키는 170cm, 95% 신뢰수준에서 +- 1.5cm
  • 전제: 표본평균의 분포는 정규분포를 따른다
• 가설검정 (Hypothesis Testing)
  
  • 어떤 주장이 우연인지, 통계적으로 의미있는지 검정
  • 표본 통계량이 정규분포 위에서 얼마나 '멀리' 떨어져 있는가(Z값)를 보고 판단
  • p-value → 작을수록 우연히 이렇게 튀었을 확률 낮다 → 귀무가설 기각
  • 통계검정은 대부분 정규분포나 t분포 위에서 이뤄짐

 

 

4. 정규분포 (Normal Distribution)

 

정규분포 (Normal Distribution)

• 중앙에 값이 몰리고 양 끝으로 갈수록 희박해지는 자연스러운 현상 분포
• 평균과 분산을 통해 모양이 정해진다
• 종 모양의 연속형 확률 분포
• 정규분포 특징
  • 평균 = 최빈값 = 중앙값 (대칭 구조)
  • 확률밀도함수의 전체 면적 = 1 (면적 = 확률)

 

• 정규분포가 중요한 이유
  • 현실에서는 전수조사가 어려움 → 모집단이 정규분포라고 가정하면 표본을 통해 모집단 특성 추정 가능
  • 예측 가능한 범위:
    • 평균 ± 1σ : 약 68.3%
    • 평균 ± 2σ : 약 95.4%
    • 평균 ± 3σ : 약 99.7%
    → 이 범위를 확률 해석에 활용할 수 있음
  •  예시
    • ex. 대한민국 20대 키가 정규분포(μ=170, σ=7)라면?
    • 무작위로 뽑은 20대 한 명의 키가 163 ~ 177에 들어갈 확률 : 약 68%
    • 내가 수집한 데이터 100명에 대해 163~177 비율이 68%에 가까우면 정규분포 가정이 타당함을 뒷받침할 수 있음
  • 정규분포 가정은 추론통계의 핵심 기반
  • 가설검정에서 p-value를 해석할 수 있는 전제
  • 우리가 관측한 데이터가 정규분포에 가깝다면,
    모집단도 정규분포를 따른다고 추정하고 통계 분석 진행

 

표준화 (Standardization)

• 정규분포의 기준선을 하나로 통일하는 작업
• Z-score: 내 점수가 평균에서 얼마나 떨어져 있는지에 대한 상대적 위치
  • Z = 1.0 → 평균보다 1σ만큼 큼 → 상위 약 15.9%
  • Z = -2.0 → 평균보다 2σ만큼 작음 → 하위 약 2.3%

 

표준정규분포

• 평균 0, 표준편차 1인 정규분포
• Z ~ N(0, 1)
• 모든 정규분포는 Z변환을 통해 표준정규분포로 바꿀 수 있음
• Z 분포 알면 →  Z 테이블 한 장으로 확률 계산 가능 → 통계 검정에서 비교 기준으로 사용
• Z값(표준점수)를 이용해 다양한 정규분포의 누적확률을 하나의 표로 계산

 

 

자료 출처

스파르타 코딩클럽 데이터 Docs 통계 세션